上一篇介绍了RMA算法的背景校正部分。接下来是归一化和最终计算过程。

首先是归一化：

归一化就是将不同组之间的数据统一。因为组之间的数据虽然经过背景校正之后去除了部分噪音。

但是如果某一组自身因为内因或者外因导致的整体波动是没法去除的，如果不去除，会发现组间是不能比较的，因为某一组整体增加和减少会导致组与组之间的大小关系被破坏了，为此引入了归一化。

RMA算法之中归一化采用的是quantile normolization算法，这个算法的步骤如下：

首先假设我们有如下的矩阵：

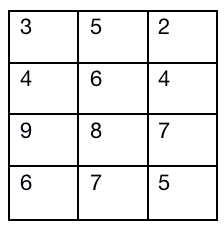该组能够看到第一列之中9比6大 第二列之中8比7大 可见每一个探针的大小关系是存在的，但是第一列的9比第二列的8大，第一列的6却比第二列的7小，这种组间的比较就显得很没有意义，因为组内存在着整体的波动。

我们按照列中从大到小排序：

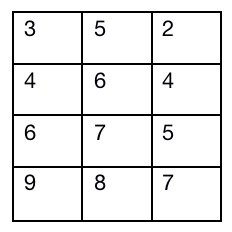
之后我们求出每一行的平均数：

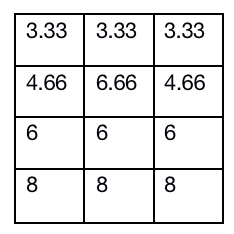
将平均数按照原来矩阵的大小顺序放回，也就是放回到排序前的位置：

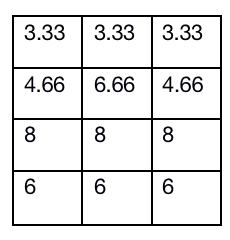
很显然数据的大小关系被保留了，而且使得本身组间不能比较的现在可以进行比较了，虽然我的数据太好看了，但是足以说明这个算法的意义。

接下来是summarization过程，采用的是median polish算法：

我们还是先说明为什么要进行summary，因为虽然我们进行了背景去噪，组间归一，但是还是存在一些没有去处的噪音。

但是这个时候的数据可以说已经具有一定的统计意义了，但是能不能做的更好呢？

所以我们在这种已经具有一定统计意义的数据上再进行一步处理，我们有理由相信每一行，也就是每一个探针的结果的中位数，相比起其他位置的数字而言更具有普世意义，所以我们作如下处理：

我们还是之前的矩阵，第四列是每一行的中位数，不是新的组哈！！：

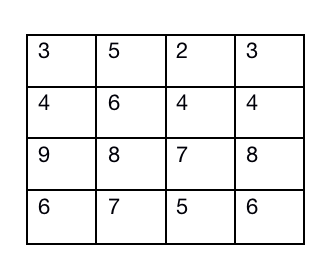
我们将每一行都减去该行的中位数：

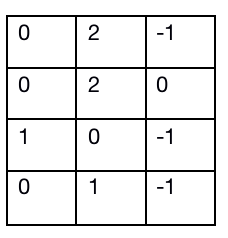
之后我们同样在在上面这个矩阵上按照列进行这个操作：

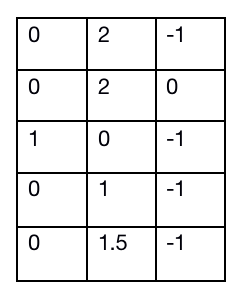第五行是中位数

每一列都减去中位数

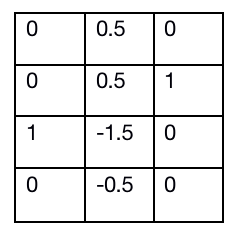
那么这个得到的矩阵的意义是什么呢？因为我们认为中位数是某种意义上的合理结果，所以减去中位数之后留下的就是噪音，

进行两次的目的是尽量的减少中位数自身也是有噪音的影响。

所以再把原矩阵减去这个最后的矩阵得到：

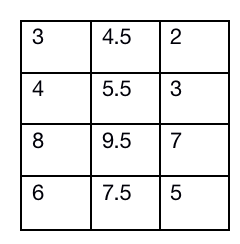
我们会看来原来矩阵第一组，也就是第一列之中和第二列之中比较时，9比8大但是6比7小，在处理出后8比9.5小，6比7.5小，可以说再一次使得数据更加统一了。可见这个过程的意义。

处理前：                                                  处理后：

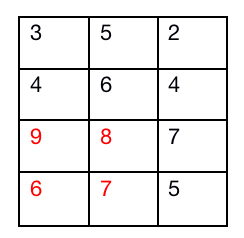
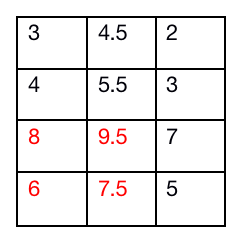
至此，我们的RMA算法算是彻底的介绍完了。